Skip to contents

dodgr

Mark Padgham

2024-12-06

Source: vignettes/dodgr.Rmd
dodgr.Rmd

1 Background: Directed Graphs

dodgr is an R package for calculating Distances On Directed Graphs. It does so very efficiently, and is able to process larger graphs than many other comparable R packages. Skip straight to the Intro if you know what directed graphs are (but maybe make a brief stop-in to Dual-Weighted Directed Graphs below.) Directed graphs are ones in which the “distance” (or some equivalent measure) from A to B is not necessarily equal to that from B to A. In Fig. 1, for example, the weights between the graph vertices (A, B, C, and D) differ depending on the direction of travel, and it is only possible to traverse the entire graph in an anti-clockwise direction.

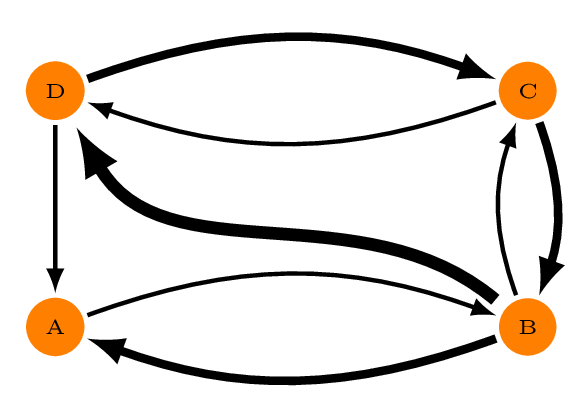
Graphs in dodgr are represented by simple flat data.frame objects, so the graph of Fig. 1, presuming the edge weights to take values of 1, 2, and 3, would be,

##   from to d
## 1    A  B 1
## 2    B  A 2
## 3    B  C 1
## 4    B  D 3
## 5    C  B 2
## 6    C  D 1
## 7    D  C 2
## 8    D  A 1

The primary function of dodgr is dodgr_dists, which calculates pair-wise shortest distances between all vertices of a graph.

dodgr_dists (graph)
##   A B C D
## A 0 1 2 3
## B 2 0 1 2
## C 2 2 0 1
## D 1 2 2 0
dodgr_dists (graph, from = c ("A", "C"), to = c ("B", "C", "D"))
##   B C D
## A 1 2 3
## C 2 0 1

1.1 Dual-Weighted Directed Graphs

Shortest-path distances on weighted graphs can be calculated using a number of other R packages, such as igraph or e1071. dodgr comes into its own through its ability to trace paths through dual-weighted directed graphs, illustrated in Fig. 2.

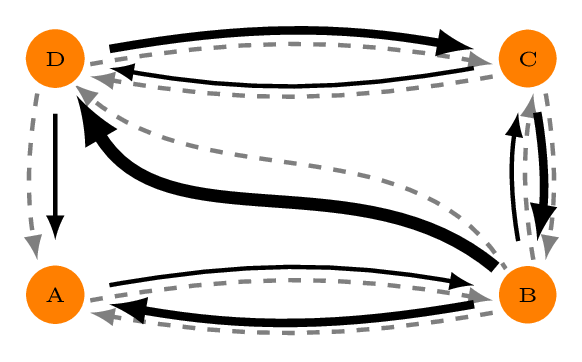
Dual-weighted directed graphs are common in many areas, a foremost example being routing through street networks. Routes through street networks depends on mode of transport: the route a pedestrian might take will generally differ markedly from the route the same person might take if behind the wheel of an automobile. Routing through street networks thus generally requires each edge to be specified with two weights or distances: one quantifying the physical distance, and a second weighted version reflecting the mode of transport (or some other preferential weighting).

dodgr calculates shortest paths using one set of weights (called “weights” or anything else starting with “w”), but returns the actual lengths of them using a second set of weights (called “distances”, or anything else starting with “d”). If no weights are specified, distances alone are used both for routing and final distance calculations. Consider that the weights and distances of Fig. 2 are the black and grey lines, respectively, with the latter all equal to one. In this case, the graph and associated shortest distances are,

##   from to w d
## 1    A  B 1 1
## 2    B  A 2 1
## 3    B  C 1 1
## 4    B  D 3 1
## 5    C  B 2 1
## 6    C  D 1 1
## 7    D  C 2 1
## 8    D  A 1 1
##   A B C D
## A 0 1 2 2
## B 1 0 1 1
## C 2 1 0 1
## D 1 2 1 0

Note that even though the shortest “distance” from A to D is actually A→\toB→\toD with a distance of only 2, that path has a weighted distance of 1 + 3 = 4. The shortest weighted path is A→\toB→\toC→\toD, with a distance both weighted and unweighted of 1 + 1 + 1 = 3. Thus d(A,D) = 3 and not 2.

2 Introduction to dodgr

Although the package has been intentionally developed to be adaptable to any kinds of networks, most of the applications illustrated here concern street networks, and also illustrate several helper functions the package offers for working with street networks. The basic graph object of dodgr is nevertheless arbitrary, and need only minimally contain three or four columns as demonstrated in the simple examples at the outset.

The package may be used to calculate a matrix of distances between a given set of geographic coordinates. We can start by simply generating some random coordinates, in this case within the bounding box defining the city of York in the U.K.

bb <- osmdata::getbb ("york uk")
npts <- 1000
xy <- apply (bb, 1, function (i) min (i) + runif (npts) * diff (i))
bb; head (xy)
##         min        max
## x -1.241536 -0.9215361
## y 53.799056 54.1190555
##               x        y
## [1,] -1.1713502 53.89409
## [2,] -1.2216108 54.01065
## [3,] -1.0457199 53.83613
## [4,] -0.9384666 53.93545
## [5,] -0.9445541 53.89436
## [6,] -1.1207099 54.01262

The following lines download the street network within that bounding box, weight it for pedestrian travel, and use the weighted network to calculate the pairwise distances between all of the xypoints.

net <- dodgr_streetnet (bb)
net <- weight_streetnet (net, wt_profile = "foot")
system.time (
            d <- dodgr_dists (net, from = xy, to = xy)
            )
##    user  system elapsed 
##  38.828   0.036   5.424
dim (d); range (d, na.rm = TRUE)
## [1] 1000 1000
## [1]     0.00 57021.18

The result is a matrix of 1000-by-1000 distances of up to 57km long, measured along routes weighted for optimal pedestrian travel. In this case, the single call to dodgr_distances() automatically downloaded the entire street network of York and calculated one million shortest-path distances, all in under 30 seconds.

3 Graphs and Street Networks

Although the above code is short and fast, most users will probably want more control over their graphs and routing possibilities. To illustrate, the remainder of this vignette analyses the much smaller street network of Hampi, Karnataka, India, included in the dodgr package as the dataset hampi. This data set may be re-created with the following single line:

hampi <- dodgr_streetnet ("hampi india")

Or with the equivalent version bundled with the package:

class (hampi)
## [1] "sf"         "data.frame"
class (hampi$geometry)
## [1] "sfc_LINESTRING" "sfc"
dim (hampi)
## [1] 236  15

The streetnet is an sf (Simple Features) object containing 189 LINESTRING geometries. In other words, it’s got an sf representation of 189 street segments. The R package osmplotr can be used to visualise this street network (with the help of magrittr pipe operator, %>%):

library (osmplotr)
library (magrittr)
map <- osm_basemap (hampi, bg = "gray95") %>%
    add_osm_objects (hampi, col = "gray5") %>%
    add_axes () %>%
    print_osm_map ()

The sf class data representing the street network of Hampi can then be converted into a flat data.frame object by

graph <- weight_streetnet (hampi, wt_profile = "foot")
dim (graph)
## [1] 6813   15
head (graph)
##   geom_num edge_id    from_id from_lon from_lat      to_id   to_lon   to_lat
## 1        1       1  339318500 76.47491 15.34167  339318502 76.47612 15.34173
## 2        1       2  339318502 76.47612 15.34173  339318500 76.47491 15.34167
## 3        1       3  339318502 76.47612 15.34173 2398958028 76.47621 15.34174
## 4        1       4 2398958028 76.47621 15.34174  339318502 76.47612 15.34173
## 5        1       5 2398958028 76.47621 15.34174 1427116077 76.47628 15.34179
## 6        1       6 1427116077 76.47628 15.34179 2398958028 76.47621 15.34174
##            d d_weighted highway   way_id component      time time_weighted
## 1 130.000241 130.000241    path 28565950         1 93.600174     93.600174
## 2 130.000241 130.000241    path 28565950         1 93.600174     93.600174
## 3   8.890622   8.890622    path 28565950         1  6.401248      6.401248
## 4   8.890622   8.890622    path 28565950         1  6.401248      6.401248
## 5   9.307736   9.307736    path 28565950         1  6.701570      6.701570
## 6   9.307736   9.307736    path 28565950         1  6.701570      6.701570

Note that the actual graph contains around 30 times as many edges as there are streets, indicating that each street is composed on average of around 30 individual segments. The individual points or vertices from those segments can be extracted with,

vt <- dodgr_vertices (graph)
head(vt)
##            id        x        y component n
## 1   339318500 76.47491 15.34167         1 0
## 2   339318502 76.47612 15.34173         1 1
## 4  2398958028 76.47621 15.34174         1 2
## 6  1427116077 76.47628 15.34179         1 3
## 8  7799710916 76.47634 15.34184         1 4
## 10  339318503 76.47641 15.34190         1 5
dim (vt)
## [1] 3337    5

From which we see that the OpenStreetMap representation of the streets of Hampi has 189 line segments with 2,987 unique points and 6,096 edges between those points. The number of edges per vertex in the entire network is thus,

nrow (graph) / nrow (vt)
## [1] 2.041654

A simple straight line has two edges between all intermediate nodes, and this thus indicates that the network in it’s entirety is quite simple. The data.frame resulting from weight_streetnet() is what dodgr uses to calculate shortest path routes, as will be described below, following a brief description of weighting street networks.

3.1 Graph Components

The foregoing graph object returned from weight_streetnet() also includes a $component column enumerating all of the distinct inter-connected components of the graph.

table (graph$component)
## 
##    1    2    3 
## 4649 2066   98

Components are numbered in order of decreasing size, with $component = 1 always denoting the largest component. In this case, that component contains 3,934 edges, representing 65% of the graph. There are clearly only three distinct components, but this number may be much larger for larger graphs, and may be obtained from,

length (unique (graph$component))
## [1] 3

Component numbers can be determined for any types of graph with the dodgr_components() function. For example, the following lines reduce the previous graph to a minimal (non-spatial) structure of four columns, and then (re-)calculate a fifth column of $components:

cols <- c ("edge_id", "from_id", "to_id", "d")
graph_min <- graph [, which (names (graph) %in% cols)]
graph_min <- dodgr_components (graph_min)
head (graph_min)
##   edge_id    from_id      to_id          d component
## 1       1  339318500  339318502 130.000241         1
## 2       2  339318502  339318500 130.000241         1
## 3       3  339318502 2398958028   8.890622         1
## 4       4 2398958028  339318502   8.890622         1
## 5       5 2398958028 1427116077   9.307736         1
## 6       6 1427116077 2398958028   9.307736         1

The component column column can be used to select or filter any component in a graph. It is particularly useful to ensure routing calculations consider only connected vertices through simply removing all minor components:

graph_connected <- graph [graph$component == 1, ]

This is explored further below (under Distance Matrices).

3.2 Weighting Profiles

Dual-weights for street networks are generally obtained by multiplying the distance of each segment by a weighting factor reflecting the type of highway. As demonstrated above, this can be done easily within dodgr with the weight_streetnet() function, which applies the named weighting profiles included with the dodgr package to OpenStreetMap networks extracted with the osmdata package.

This function uses the internal data dodgr::weighting_profiles, which is a list of three items:

  1. weighting_profiles;
  2. surface_speeds; and
  3. penalties

Most of these data are used to calculate routing times with the dodgr_times function, as detailed in an additional vignette. The only aspects relevant for distances are the profiles themselves, which assign preferential weights to each distinct type of highway.

wp <- weighting_profiles$weighting_profiles
names (wp)
## [1] "name"      "way"       "value"     "max_speed"
class (wp)
## [1] "data.frame"
unique (wp$name)
##  [1] "foot"       "horse"      "wheelchair" "bicycle"    "moped"     
##  [6] "motorcycle" "motorcar"   "goods"      "hgv"        "psv"
wp [wp$name == "foot", ]
##    name            way value max_speed
## 1  foot       motorway  0.00        NA
## 2  foot          trunk  0.40        NA
## 3  foot        primary  0.50         5
## 4  foot      secondary  0.60         5
## 5  foot       tertiary  0.70         5
## 6  foot   unclassified  0.80         5
## 7  foot    residential  0.90         5
## 8  foot        service  0.90         5
## 9  foot          track  0.95         5
## 10 foot       cycleway  0.95         5
## 11 foot           path  1.00         5
## 12 foot          steps  0.80         2
## 13 foot          ferry  0.20         5
## 14 foot  living_street  0.95         5
## 15 foot      bridleway  1.00         5
## 16 foot        footway  1.00         5
## 17 foot     pedestrian  1.00         5
## 18 foot  motorway_link  0.00        NA
## 19 foot     trunk_link  0.40        NA
## 20 foot   primary_link  0.50         5
## 21 foot secondary_link  0.60         5
## 22 foot  tertiary_link  0.70         5

Each profile is defined by a series of percentage weights quantifying highway-type preferences for a particular mode of travel. The distinct types of highways within the Hampi graph obtained above can be tabulated with:

table (graph$highway)
## 
## living_street          path       primary   residential     secondary 
##            20          3557           430           196           560 
##       service         steps         track  unclassified 
##           256           108           914           772

Hampi is unlike most other human settlements on the planet in being a Unesco World Heritage area in which automobiles are generally prohibited. Accordingly, numbers of "footway", "path", and "pedestrian" ways far exceed typical categories denoting automobile traffic ("primary", "residential", "tertiary")

It is also possible to use other types of (non-OpenStreetMap) street networks, an example of which is the os_roads_bristol data provided with the package. “OS” is the U.K. Ordnance Survey, and these data are provided as a Simple Features (sf) data.frame with a decidedly different structure to osmdata data.frame objects:

names (hampi) # many fields manually removed to reduce size of this object
##  [1] "osm_id"        "bicycle"       "covered"       "foot"         
##  [5] "highway"       "incline"       "motorcar"      "motorcycle"   
##  [9] "motor_vehicle" "oneway"        "surface"       "tracktype"    
## [13] "tunnel"        "width"         "geometry"
names (os_roads_bristol)
##  [1] "fictitious" "identifier" "class"      "roadNumber" "name1"     
##  [6] "name1_lang" "name2"      "name2_lang" "formOfWay"  "length"    
## [11] "primary"    "trunkRoad"  "loop"       "startNode"  "endNode"   
## [16] "structure"  "nameTOID"   "numberTOID" "function."  "geometry"

The latter may be converted to a dodgr network by first specifying a weighting profile, here based on the formOfWay column:

colnm <- "formOfWay"
table (os_roads_bristol [[colnm]])
## 
## Collapsed Dual Carriageway           Dual Carriageway 
##                         14                          6 
##         Single Carriageway                  Slip Road 
##                          1                          8
wts <- data.frame (name = "custom",
                   way = unique (os_roads_bristol [[colnm]]),
                   value = c (0.1, 0.2, 0.8, 1))
net <- weight_streetnet (os_roads_bristol, wt_profile = wts,
                         type_col = colnm, id_col = "identifier")

The resultant net object contains the street network of os_roads_bristol weighted by the specified profile, and in a format suitable for submission to any dodgr routine.

3.3 Random Sub-Graphs

The dodgr packages includes a function to select a random connected portion of graph including a specified number of vertices. This function is used in the compare_heaps() function described below, but is also useful for general statistical analyses of large graphs which may otherwise take too long to compute.

graph_sub <- dodgr_sample (graph, nverts = 100)
nrow (graph_sub)
## [1] 199

The random sample has around twice as many edges as vertices, in accordance with the statistics calculated above.

nrow (dodgr_vertices (graph_sub))
## [1] 100

4 Distance Matrices: dodgr_dists()

As demonstrated at the outset, an entire network can simply be submitted to dodgr_distances(), in which case a square matrix will be returned containing pair-wise distances between all vertices. Doing that for the graph of York will return a square matrix of around 90,000-times-90,000 (or 8 billion) distances. It might be possible to do that on some computers, but is possibly neither recommended nor desirable. The dodgr_distances() function accepts additional arguments of from and to defining points from and to which distances are to be calculated. If only from is provided, a square matrix is returned of pair-wise distances between all listed points.

4.1 Aligning Routing Points to Graphs

For spatial graphs—that is, those containing columns of latitudes and longitudes (or “x” and “y”)—routing points can be represented by a simple matrix of arbitrary latitudes and longitudes (or, again, “x” and “y”). dodgr_distances() will map these points to the closest network points, and return corresponding shortest-path distances. This may be illustrated by generating random points within the bounding box of the above map of Hampi. As demonstrated above, the coordinates of all vertices may be extracted with the dodgr_vertices() function, enabling random points to be generated with the following lines:

vt <- dodgr_vertices (graph)
n <- 100 # number of points to generate
xy <- data.frame (x = min (vt$x) + runif (n) * diff (range (vt$x)),
                  y = min (vt$y) + runif (n) * diff (range (vt$y)))

Submitting these to dodgr_distances() as points from which to route will generate a distance matrix from each of these 100 points to every other point in the graph:

d <- dodgr_dists (graph, from = xy)
dim (d); range (d, na.rm = TRUE)
## [1]  100 3337
## [1]     0.00 14926.04

If the to argument is also specified, the matrix returned will have rows matching from and columns matching to

d <- dodgr_dists (graph, from = xy, to = xy [1:10, ])
dim (d)
## [1] 100  10

Some of the resultant distances in the above cases are NA because the points were sampled from the entire bounding box, and the street network near the boundaries may be cut off from the rest. As demonstrated above, the weight_streetnet() function returns a component vector, and such disconnected edges will have graph$component > 1, because graph$component == 1 always denotes the largest connected component. This means that the graph can always be reduced to the single largest component with the following single line:

graph_connected <- graph [graph$component == 1, ]

A distance matrix obtained from running dodgr_distances on graph_connected should generally contain no NA values, although some points may still be effectively unreachable due to one-way connections (or streets). Thus, routing on the largest connected component of a directed graph ought to be expected to yield the minimal number of NA values, which may sometimes be more than zero. Note further that spatial routing points (expressed as from and/or to arguments) will in this case be mapped to the nearest vertices of graph_connected, rather than the potentially closer nearest points of the full graph. This may make the spatial mapping of routing points less accurate than results obtained by repeating extraction of the street network using an expanded bounding box. For automatic extraction of street networks with dodgr_distances(), the extent by which the bounding box exceeds the range of routing points (from and to arguments) is determined by an extra parameter expand, quantifying the relative extent to which the bounding box should exceed the spatial range of the routing points. This is illustrated in the following code which calculates distances between 100 random points:

bb <- osmdata::getbb ("york uk")
npts <- 100
xy <- apply (bb, 1, function (i) min (i) + runif (npts) * diff (i))

routed_points <- function (expand = 0, pts) {

    gr0 <- dodgr_streetnet (pts = pts, expand = expand) %>%
        weight_streetnet ()
    d0 <- dodgr_dists (gr0, from = pts)
    length (which (is.na (d0))) / length (d0)
}
vapply (c (0, 0.05, 0.1, 0.2), function (i) routed_points (i, pts = xy),
        numeric (1))
## [1] 0.04007477 0.02326452 0.02131992 0.00000000

With a street network that precisely encompasses the submitted routing points (expand = 0), 4% of pairwise distances are unable to be calculated; with a bounding box expanded to 5% larger than the submitted points, this is reduced to 2.3%, and with expansion to 20%, all points can be connected.

For non-spatial graphs, from and to must match precisely on to vertices named in the graph itself. In the graph considered above, these vertex names were contained in the columns, from_id and to_id. The minimum that a dodgr graph requires is,

head (graph [, names (graph) %in% c ("from_id", "to_id", "d")])
##      from_id      to_id          d
## 1  339318500  339318502 130.000241
## 2  339318502  339318500 130.000241
## 3  339318502 2398958028   8.890622
## 4 2398958028  339318502   8.890622
## 5 2398958028 1427116077   9.307736
## 6 1427116077 2398958028   9.307736

in which case the from values submitted to dodgr_dists() (and to, if given) must directly name the vertices in the from_id and to_id columns of the graph. This is illustrated in the following code:

graph_min <- graph [, names (graph) %in% c ("from_id", "to_id", "d")]
fr <- sample (graph_min$from_id, size = 10) # 10 random points
to <- sample (graph_min$to_id, size = 20)
d <- dodgr_dists (graph_min, from = fr, to = to)
dim (d)
## [1] 10 20

The result is a 10-by-20 matrix of distances between these named graph vertices.

4.2 Shortest Path Calculations: Priority Queues

dodgr uses an internal library Shane Saunders (2004) for the calculation of shortest paths using a variety of priority queues (see Miller 1960 for an overview). In the context of shortest paths, priority queues determine the order in which a graph is traversed (Tarjan 1983), and the choice of priority queue can have a considerable effect on computational efficiency for different kinds of graphs (Johnson 1977). In contrast to dodgr, most other R packages for shortest path calculations do not use priority queues, and so may often be less efficient. Shortest path distances can be calculated in dodgr with priority queues that use the following heaps:

  1. Binary heaps;
  2. Fibonacci heaps (Fredman and Tarjan 1987);
  3. Trinomial and extended trinomial heaps (Takaoka 2000); and
  4. 2-3 heaps (Takaoka 1999).

Differences in how these heaps operate are often largely extraneous to direct application of routing algorithms, even though heap choice may strongly affect performance. To avoid users needing to know anything about algorithmic details, dodgr provides a function compare_heaps() to which a particular graph may be submitted in order to determine the optimal kind of heap.

The comparisons are actually made on a randomly selected sub-component of the graph containing a defined number of vertices (with a default of 1,000, or the entire graph if it contains fewer than 1,000 vertices).

compare_heaps (graph, nverts = 100)
## Loading required namespace: bench
## Loading required namespace: igraph
## # A tibble: 11 × 6
##    expression                 min   median `itr/sec` mem_alloc `gc/sec`
##    <bch:expr>            <bch:tm> <bch:tm>     <dbl> <bch:byt>    <dbl>
##  1 BHeap                   1.86ms   1.94ms      514.    45.9KB     16.1
##  2 FHeap                   1.88ms   1.95ms      508.    45.9KB     15.1
##  3 TriHeap                  1.9ms   1.98ms      503.    45.9KB     15.2
##  4 TriHeapExt              1.73ms   1.78ms      557.    48.9KB     17.5
##  5 Heap23                   1.9ms   1.96ms      503.    45.9KB     15.1
##  6 BHeap_contracted        1.68ms   1.75ms      565.      19KB     19.9
##  7 FHeap_contracted        1.69ms   1.76ms      560.      19KB     17.5
##  8 TriHeap_contracted      1.69ms   1.76ms      565.      19KB     17.5
##  9 TriHeapExt_contracted   1.46ms   1.51ms      655.      19KB     19.8
## 10 Heap23_contracted       1.68ms   1.77ms      564.      19KB     17.6
## 11 igraph                672.68µs 713.71µs     1383.   482.6KB     22.2

The key column of that data.frame is relative, which quantifies the relative performance of each test in relation to the best which is given a score of 1. dodgr using the default heap = "BHeap", which is a binary heap priority queue, performs faster than igraph (Csardi and Nepusz 2006) for these graphs. Different kind of graphs will perform differently with different priority queue structures, and this function enables users to empirically discern the optimal heap for their kind of graph.

Note, however, that this is not an entirely fair comparison, because dodgr calculates dual-weighted distances, whereas igraph—and indeed all other R packages—only directly calculate distances based on a single set of weights. Implementing dual-weighted routing in these cases requires explicitly re-tracing all paths and summing the second set of weights along each path. A time comparison in that case would be very strongly in favour of dodgr. Moreover, dodgr can convert graphs to contracted form through removing redundant vertices, as detailed in the following section. Doing so greatly improves performance with respect to igraph.

For those wishing to do explicit comparisons themselves, the following code generates the igraph equivalent of dodgr_distances(), although of course for single-weighted graphs only:

v <- dodgr_vertices (graph)
pts <- sample (v$id, 1000)
igr <- dodgr_to_igraph (graph)
d <- igraph::distances (igr, v = pts, to = pts, mode = "out")

5 Graph Contraction

A further unique feature of dodgr is the ability to remove redundant vertices from graphs (see Fig. 3), thereby speeding up routing calculations.

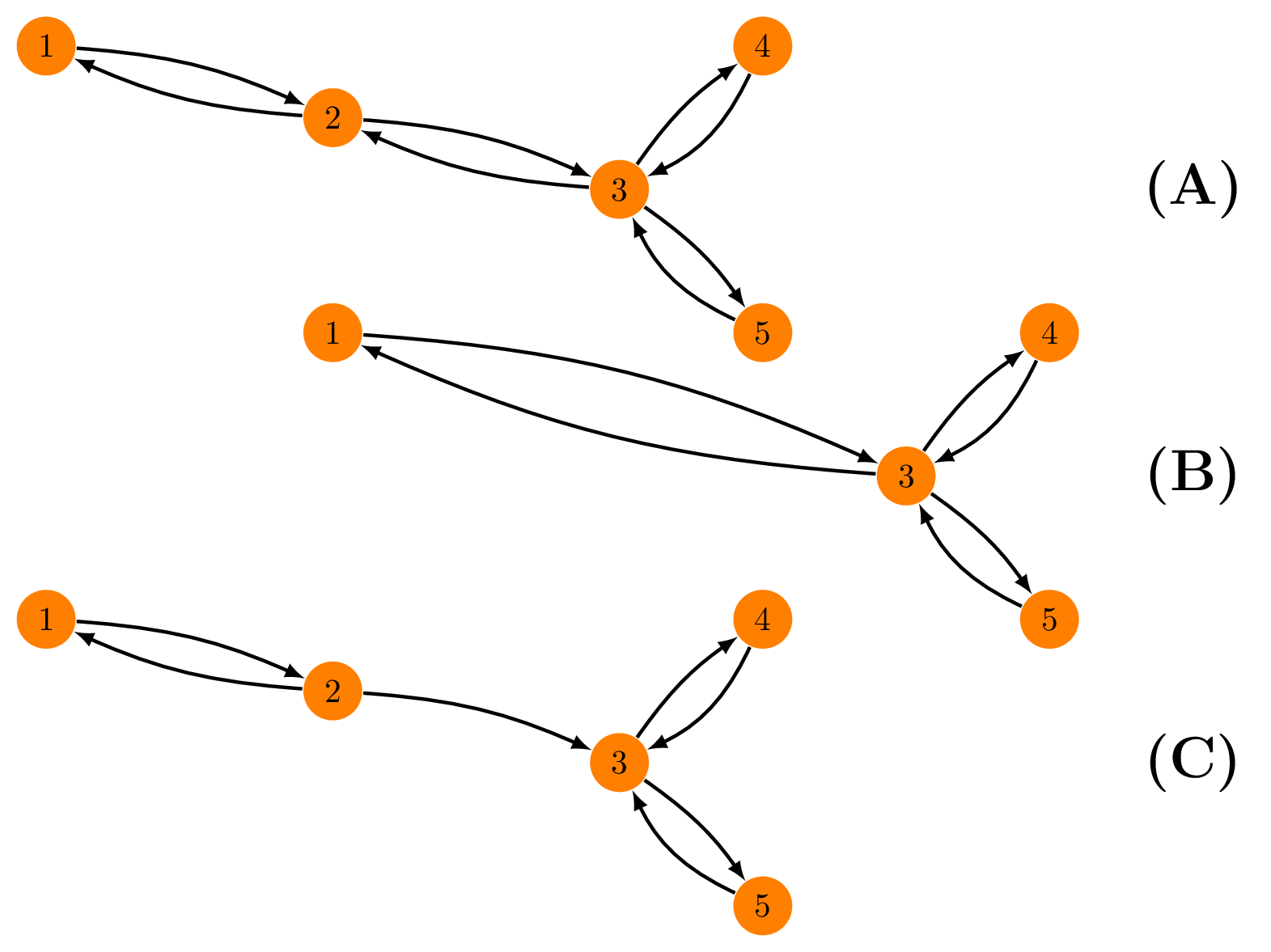
In Fig. 3(A), the only way to get from vertex 1 to 3, 4 or 5 is through C. The intermediate vertex B is redundant for routing purposes (and than to or from that precise point) and may simply be removed, with directional edges inserted directly between vertices 1 and 3. This yields the equivalent contracted graph of Fig. 3(B), in which, for example, the distance (or weight) between 1 and 3 is the sum of previous distances (or weights) between 1 →\to 2 and 2 →\to 3. Note that if one of the two edges between, say, 3 and 2 were removed, vertex 2 would no longer be redundant (Fig. 3(C)).

Different kinds of graphs have different degrees of redundancy, and even street networks differ, through for example dense inner-urban networks generally being less redundant than less dense extra-urban or rural networks. The contracted version of a graph can be obtained with the function dodgr_contract_graph(), illustrated here with the York example from above.

grc <- dodgr_contract_graph (graph)

The function dodgr_contract_graph() returns the contracted version of the original graph, containing the same number of columns, but with each row representing an edge between two junction vertices (or between the submitted verts, which may or may not be junctions). Relative sizes are

nrow (graph); nrow (grc); nrow (grc) / nrow (graph)
## [1] 6813
## [1] 748
## [1] 0.1097901

equivalent to the removal of around 90% of all edges. The difference in routing efficiency can then be seen with the following code

from <- sample (grc$from_id, size = 100)
to <- sample (grc$to_id, size = 100)
bench::mark (
    full = dodgr_dists (graph, from = from, to = to),
    contracted = dodgr_dists (grc, from = from, to = to),
    check = FALSE # numeric rounding errors can lead to differences
    )
## # A tibble: 2 × 6
##   expression      min   median `itr/sec` mem_alloc `gc/sec`
##   <bch:expr> <bch:tm> <bch:tm>     <dbl> <bch:byt>    <dbl>
## 1 full        13.19ms   13.8ms      71.6    1.24MB     2.05
## 2 contracted   2.47ms    2.7ms     357.   280.59KB     2.02

And contracting the graph has a similar effect of speeding up pairwise routing between these 100 points. All routing algorithms scale non-linearly with size, and relative improvements in efficiency will be even greater for larger graphs.

5.1 Routing on Contracted Graphs

Routing is often desired between defined points, and these points may inadvertently be removed in graph contraction. The dodgr_contract_graph() function accepts an additional argument specifying vertices to keep within the contracted graph. This list of vertices must directly match the vertex ID values in the graph.

The following code illustrates how to retain specific vertices within contracted graphs:

grc <- dodgr_contract_graph (graph)
nrow (grc)
## [1] 748
verts <- sample (dodgr_vertices (graph)$id, size = 100)
head (verts) # a character vector
## [1] "8632923846" "2627461397" "1143452334" "2195424978" "1398748003"
## [6] "2632626808"
grc <- dodgr_contract_graph (graph, verts)
nrow (grc)
## [1] 940

Retaining the nominated vertices yields a graph with considerably more edges than the fully contracted graph excluding these vertices. The dodgr_distances() function can be applied to the latter graph to obtain accurate distances precisely routed between these points, yet using the speed advantages of graph contraction.

6 Shortest Paths

Shortest paths can also be extracted with the dodgr_paths() function. For given vectors of from and to points, this returns a nested list so that if,

dp <- dodgr_paths (graph, from = from, to = to)

then dp [[i]] [[j]] will contain the path from from [i] to to [j]. The paths are represented as sequences of vertex names. Consider the following example,

graph <- weight_streetnet (hampi, wt_profile = "foot")
head (graph)
##   geom_num edge_id    from_id from_lon from_lat      to_id   to_lon   to_lat
## 1        1       1  339318500 76.47491 15.34167  339318502 76.47612 15.34173
## 2        1       2  339318502 76.47612 15.34173  339318500 76.47491 15.34167
## 3        1       3  339318502 76.47612 15.34173 2398958028 76.47621 15.34174
## 4        1       4 2398958028 76.47621 15.34174  339318502 76.47612 15.34173
## 5        1       5 2398958028 76.47621 15.34174 1427116077 76.47628 15.34179
## 6        1       6 1427116077 76.47628 15.34179 2398958028 76.47621 15.34174
##            d d_weighted highway   way_id component      time time_weighted
## 1 130.000241 130.000241    path 28565950         1 93.600174     93.600174
## 2 130.000241 130.000241    path 28565950         1 93.600174     93.600174
## 3   8.890622   8.890622    path 28565950         1  6.401248      6.401248
## 4   8.890622   8.890622    path 28565950         1  6.401248      6.401248
## 5   9.307736   9.307736    path 28565950         1  6.701570      6.701570
## 6   9.307736   9.307736    path 28565950         1  6.701570      6.701570

The columns of from_id and to_id contain the names of the vertices. To extract shortest paths between some of these, first take some small samples of from and to points, and submit them to dodgr_paths():

from <- sample (graph$from_id, size = 10)
to <- sample (graph$to_id, size = 5)
dp <- dodgr_paths (graph, from = from, to = to)
length (dp)
## [1] 10

The result (dp) is a list of 10 items, each of which contains 5 vectors. An example is,

dp [[1]] [[1]]
##   [1] "5974426302" "5351820880" "5974426297" "5351820881" "5974426291"
##   [6] "5351820882" "5351820883" "5351820884" "5974426298" "5351820885"
##  [11] "5974426292" "5974426286" "5351820886" "5351820887" "5974426278"
##  [16] "5351820888" "5351820889" "5351820890" "5351820891" "5974426256"
##  [21] "5351820892" "5351820919" "5351820893" "5351820895" "5974426293"
##  [26] "5974426287" "5351820897" "5351820899" "5974426279" "5351820900"
##  [31] "5974426271" "5351820901" "5351820902" "5351820903" "5351820904"
##  [36] "5351820905" "5351820906" "5351820907" "5351820908" "5974426280"
##  [41] "5351820909" "5351820910" "5974426272" "5974426265" "5351820911"
##  [46] "5974426258" "5351820913" "5351820914" "5351820915" "5351820916"
##  [51] "2588146068" "7793361770" "7793361768" "7793361769" "7793361767"
##  [56] "2588146127" "2588146020" "2588146125" "7793361766" "7793361765"
##  [61] "2588146098" "2588146103" "2588146101" "2588146089" "2588146081"
##  [66] "2588146050" "2588146042" "2588146120" "2588146091" "2588146032"
##  [71] "2398957747" "2398957748" "1390214349" "2398957751" "2398957754"
##  [76] "286632888"  "2398957758" "2398957760" "2398957761" "2398957762"
##  [81] "2398957764" "2398957765" "2398957768" "2398957774" "2398957775"
##  [86] "1390214918" "2398957782" "2398957783" "286632889"  "1390214848"
##  [91] "2398957792" "2398957793" "286632890"  "2398957794" "2398957795"
##  [96] "2398957796" "2398957797" "2398957798" "340148006"  "340148007" 
## [101] "2398957809" "2398957814" "286632895"  "1390214618" "2398957831"
## [106] "2398957835" "286632896"  "2398957838" "1604033309" "2398957841"
## [111] "2398957842" "2398957844" "338512693"  "2627477006" "4035136503"
## [116] "338904393"  "1054864311" "2398957856" "286632897"  "2398957854"
## [121] "2398957851" "2398957849" "3921515457" "338904394"  "980400489" 
## [126] "1715805187" "2398957846" "286632898"  "338908580"  "338908581" 
## [131] "338908589"  "2398957843" "338904455"  "3697938024" "8616917041"
## [136] "3697938023" "8616917040" "8616917039" "3697938021" "3697938022"
## [141] "3697938335" "3697938334" "3697938333" "3697938338" "3697938337"
## [146] "3697938336" "3697938331" "3697938330" "3697938329" "3697938332"
## [151] "3697938328" "3697938327" "3697938326" "3697938325" "3697937571"
## [156] "3697937610" "3697937615" "3697937614" "3697937613" "3697937611"
## [161] "3697937612" "3697937616" "3697937609" "3697937608" "3697937607"
## [166] "1376769110" "1376768521" "7799710961" "7799710962" "1376768883"
## [171] "7799710963" "1376768309" "7799710965" "1376768766" "7799710964"
## [176] "1376769150" "1376768556" "7799710966" "1376768915" "7799710967"
## [181] "7799710968" "7799710969" "1376769206" "7799710974" "7799710970"
## [186] "1376768611" "7799710973" "7799710976" "1376768971" "7799710975"
## [191] "1376768395" "7799710977" "7799710978" "7799710979" "1376768859"
## [196] "7799710980" "1376769235" "7799710981" "7799710982" "1376768641"
## [201] "7799710983" "7799710984" "1376769001" "1376768341" "7799710985"
## [206] "7799710986" "1376768709" "1376769061" "1376768498" "7799710996"
## [211] "7799710994" "7799710995" "1376768949" "1376768372" "7799710997"
## [216] "7799710998" "1376768741" "1376769127" "7799711001" "7799710999"
## [221] "7799711000" "1376768426" "7799711003" "7799711002" "7799711004"
## [226] "1376768796" "7799711005" "7799711006" "1376769182" "7799711009"
## [231] "7799711007" "7799711008" "1376768589" "7799711010" "1376769033"
## [236] "1376768471" "7799711013" "7799711012" "1376768835" "1376769213"
## [241] "7799711016" "7799711014" "7799711015" "1376768528" "7799711017"
## [246] "1376768891" "1376768317" "7799711020" "7799711018" "7799711019"
## [251] "1376768683" "7799711021" "7799711022" "1376769157"

For spatial graphs, the coordinates of these paths can be obtained by extracting the vertices with dodgr_vertices() and matching the vertex IDs:

verts <- dodgr_vertices (graph)
path1 <- verts [match (dp [[1]] [[1]], verts$id), ]
head (path1)
##              id        x        y component    n
## 5636 5974426302 76.44547 15.31350         1 2786
## 5638 5351820880 76.44541 15.31355         1 2787
## 5640 5974426297 76.44532 15.31366         1 2788
## 5642 5351820881 76.44521 15.31373         1 2789
## 5644 5974426291 76.44506 15.31379         1 2790
## 5646 5351820882 76.44496 15.31379         1 2791

Paths calculated on contracted graphs will of course have fewer vertices than those calculated on full graphs.

Bibliography

Csardi, Gabor, and Tamas Nepusz. 2006. “The Igraph Software Package for Complex Network Research.” InterJournal Complex Systems: 1695. https://igraph.org.
Fredman, Michael L., and Robert Endre Tarjan. 1987. “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms.” J. ACM 34 (3): 596–615. https://doi.org/10.1145/28869.28874.
Johnson, Donald B. 1977. “Efficient Algorithms for Shortest Paths in Sparse Networks.” J. ACM 24 (1): 1–13. https://doi.org/10.1145/321992.321993.
Miller, Rupert G. 1960. “Priority Queues.” The Annals of Mathematical Statistics 31 (1): 86–103. https://projecteuclid.org/journals/annals-of-mathematical-statistics/volume-31/issue-1/Priority-Queues/10.1214/aoms/1177705990.full.
Saunders, Shane. 2004. “Improved Shortest Path Algorithms for Nearly Acyclic Graphs.” PhD thesis, Department of Computer Science; Software Engineering, University of Canterbury, New Zealand.
Saunders, S., and T. Takaoka. 2003. “Improved Shortest Path Algorithms for Nearly Acyclic Graphs.” Theoretical Computer Science 293 (3): 535--556.
Takaoka, Tadao. 1999. “Theory of 2-3 Heaps.” In Computing and Combinatorics: 5th Annual International Conference, COCOON’99 Tokyo, Japan, July 26–28, 1999 Proceedings, edited by Takano Asano, Hideki Imai, D. T. Lee, Shin-ichi Nakano, and Takeshi Tokuyama, 41–50. Springer Berlin Heidelberg. https://doi.org/10.1007/3-540-48686-0_4.
———. 2000. “Theory of Trinomial Heaps.” In Computing and Combinatorics: 6th Annual International Conference, COCOON 2000 Sydney, Australia, July 26–28, 2000 Proceedings, edited by Ding-Zhu Du, Peter Eades, Vladimir Estivill-Castro, Xuemin Lin, and Arun Sharma, 362–72. Springer Berlin Heidelberg. https://doi.org/10.1007/3-540-44968-X_36.
Tarjan, R. 1983. Data Structures and Network Algorithms. Society for Industrial; Applied Mathematics. https://doi.org/10.1137/1.9781611970265.